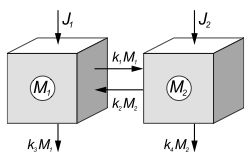
Linear two-box model
Two boxes, each with inputs from and outputs to the environment, and an exchange flux between the two boxes. Adjust the parameters by dragging them, and the initial values of the boxes by changing their size.
M1
Initial value: 0
5 0.00 M1M2
Initial value: 0
0 0.10 M2
dM1dt=5 – 0.40 M1 + 0.10 M2
dM2dt=0 + 0.40 M1 – 0.20 M2
dM2dt=0 + 0.40 M1 – 0.20 M2
0,0
50
25
75
0
250
0
0,0
250
0
250
0
The formal equations
dM1dt=J1−(k1+k3)M1+k2M2dM2dt=J2+k1M1−(k2+k4)M2